Даны дроби 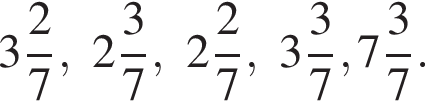 Укажите дробь, которая равна дроби
Укажите дробь, которая равна дроби ![]()
Централизованное тестирование по математике, 2014
Укажите номер рисунка, на котором изображены фигуры, симметричные относительно прямой l.
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 256°. Найдите градусную меру меньшего угла.
Результат разложения многочлена x (2a − b) + b − 2a на множители имеет вид:
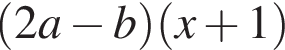
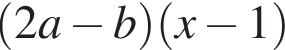
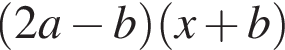
Вычислите 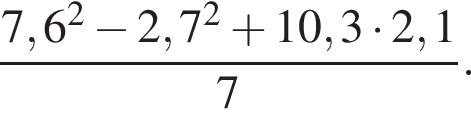
На координатной плоскости изображен параллелограмм ABCD с вершинами в узлах сетки (см.рис.). Длина диагонали BD параллелограмма равна:
Длины катетов прямоугольного треугольника являются корнями уравнения x2 − 9x + 6 = 0. Найдите площадь треугольника.
Пусть a = 3,6; b = 7,8 · 101. Найдите произведение ab и запишите его в стандартном виде.
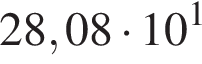
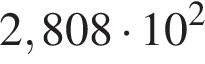
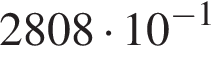

Выразите t из равенства 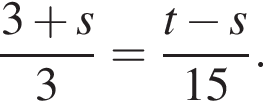
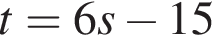



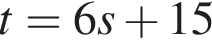
Из точки A к окружности проведены касательные AB и AC и секущая AM, проходящая через центр окружности O. Точки B, С, M лежат на окружности (см. рис.). Известно, что BK = 4, AC = 7. Найдите длину отрезка AK.
Даны два числа. Известно, что одно из них больше другого на 8. Какому условию удовлетворяет большее число x, если сумма квадратов этих чисел не меньше удвоенного квадрата большего числа?

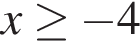

Свежие фрукты при сушке теряют a % своей массы. Укажите выражение, определяющее массу сухих фруктов (в килограммах), полученных из 60 кг свежих.
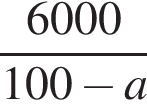
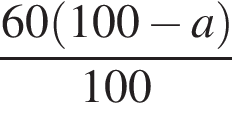
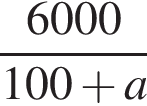
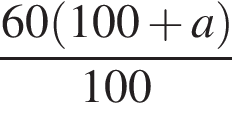
Объем конуса равен 7, а его высота равна ![]() Найдите площадь основания конуса.
Найдите площадь основания конуса.
Известно, что наименьшее значение функции, заданной формулой y = x2 + 12x + c, равно −11. Тогда значение c равно:
Строительная бригада планирует заказать фундаментные блоки у одного из трех поставщиков. Стоимость блоков и их доставки указана в таблице. При покупке какого количества блоков самыми выгодными будут условия второго поставщика?
| Поставщик | Стоимость фундаментных блоков | Стоимость доставки фундаментных блоков |
|---|---|---|
| 1 | 160 | 1300 |
| 2 | 175 | 630 |
| 3 | 200 | бесплатно |
Расположите числа 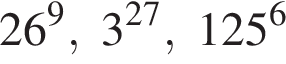 в порядке возрастания.
в порядке возрастания.
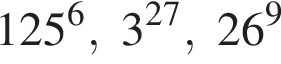
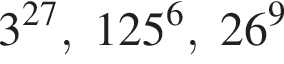
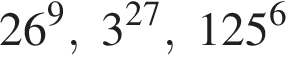
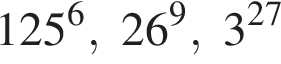
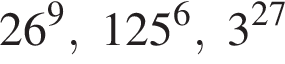
Через вершину A прямоугольного треугольника ABC (∠C = 90°) проведен перпендикуляр AK к его плоскости. Найдите расстояние от точки K до прямой BC, если AK = 2, AB = 6, BC = ![]()
Сумма корней (корень, если он единственный) уравнения 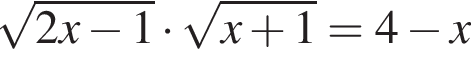 равна (равен):
равна (равен):
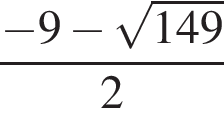
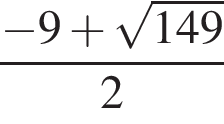
Найдите сумму целых решений (решение, если оно единственное) системы неравенств 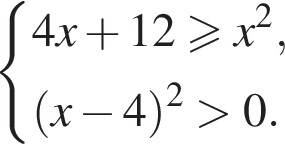
Найдите произведение большего корня на количество корней уравнения 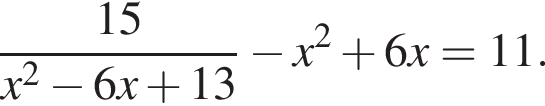
В окружность радиусом 4 вписан треугольник, длины двух сторон которого равны 6 и 4. Найдите длину высоты треугольника, проведенной к его третьей стороне.
Найдите сумму наименьшего и наибольшего целых решений неравенства 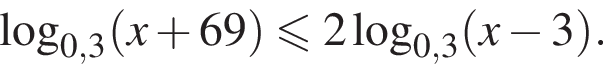
Найдите сумму (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения 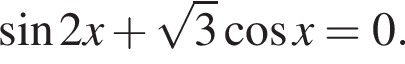
Три числа составляют геометрическую прогрессию, в которой ![]() Если второй член прогрессии уменьшить на 12, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 32, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Если второй член прогрессии уменьшить на 12, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 32, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Найдите произведение суммы корней уравнения 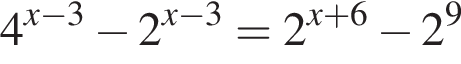 на их количество.
на их количество.
Найдите количество корней уравнения 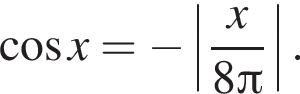
Найдите сумму целых решений неравенства 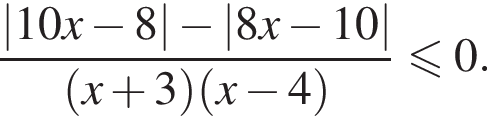
Куб вписан в правильную четырехугольную пирамиду так, что четыре его вершины находятся на боковых ребрах пирамиды, а четыре другие вершины — на ее основании. Длина стороны основания пирамиды равна 3, высота пирамиды — 2. Найдите площадь S поверхности куба. В ответ запишите значение выражения 25S.
Найдите значение выражения 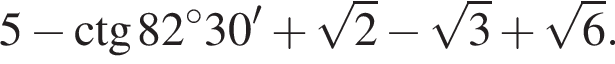
Трое рабочих (не все одинаковой квалификации) выполнили некоторую работу, работая поочередно. Сначала первый из них проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал
часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал
часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 6.
часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 6.

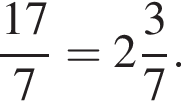
 равна 360°, поэтому четвертый угол равен 104°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 76°.
равна 360°, поэтому четвертый угол равен 104°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 76°.
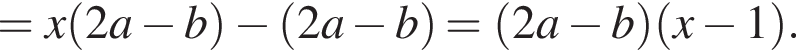

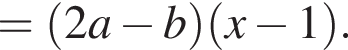
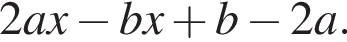
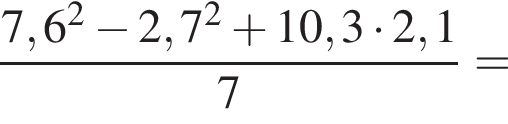
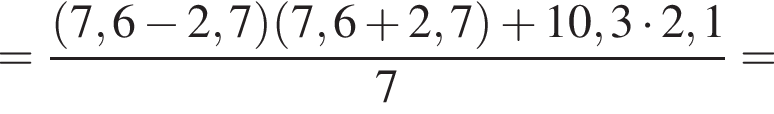
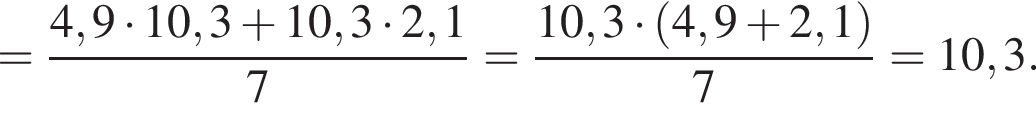
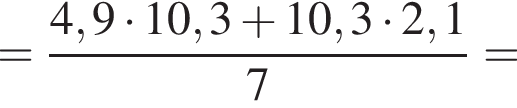
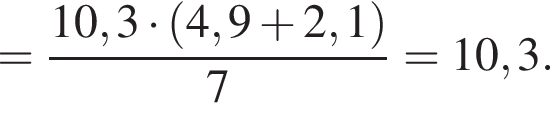
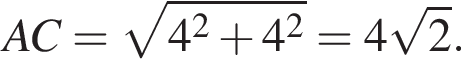
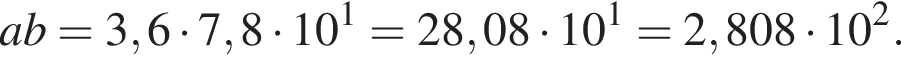
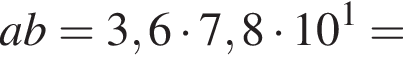
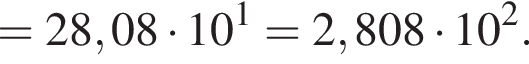
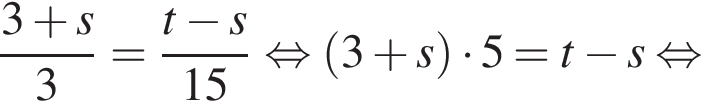
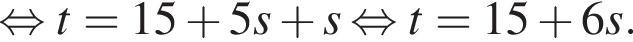
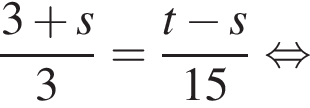
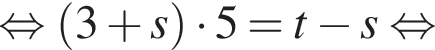

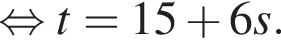
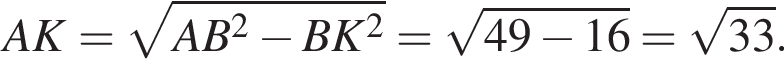
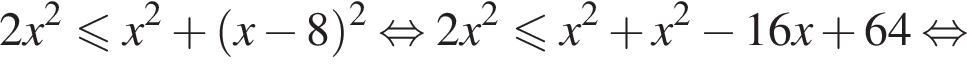

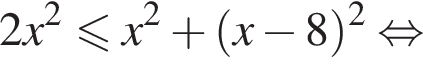
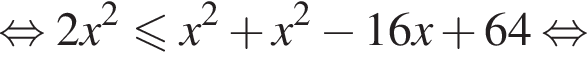
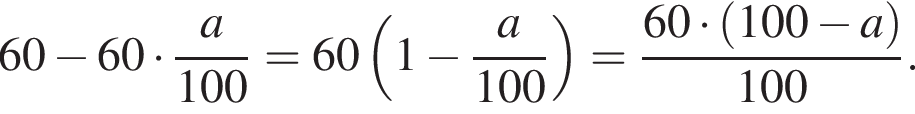
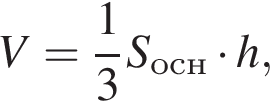 поэтому
поэтому 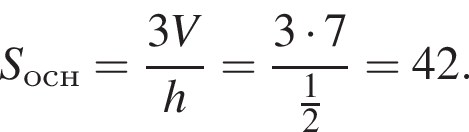
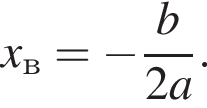 Поэтому
Поэтому 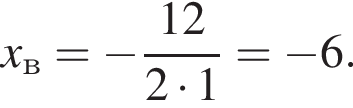 Поскольку y(xв) = −11, имеем:
Поскольку y(xв) = −11, имеем: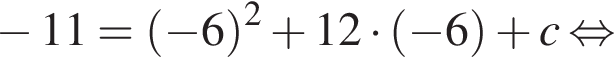


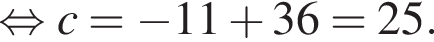
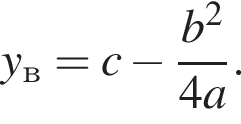
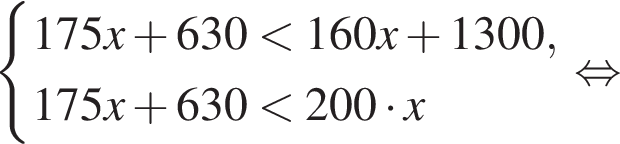
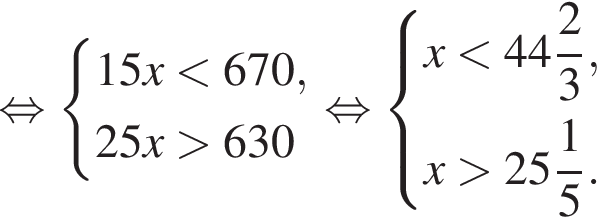
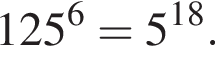 Поскольку все числа положительны, извлечем из каждого корень девятой степени и получим:
Поскольку все числа положительны, извлечем из каждого корень девятой степени и получим: 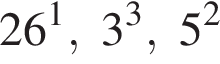 то есть числа 26, 27, 25. Так как 25 < 26 < 27, получаем
то есть числа 26, 27, 25. Так как 25 < 26 < 27, получаем 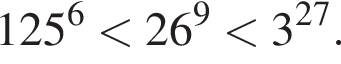
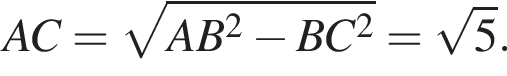 Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC
Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC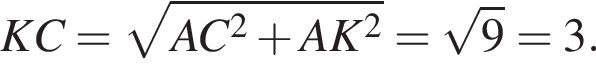
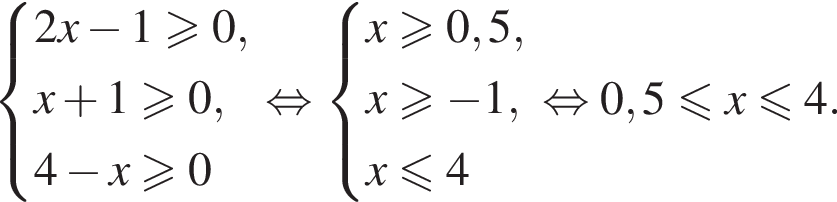
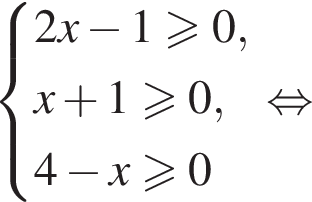
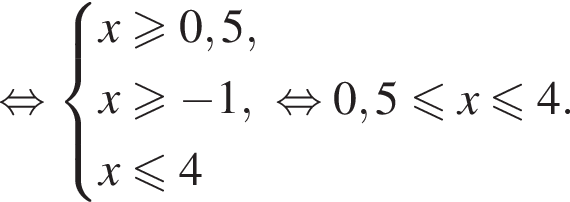
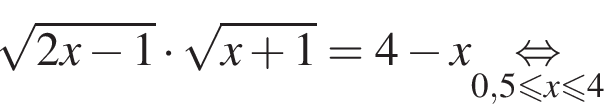
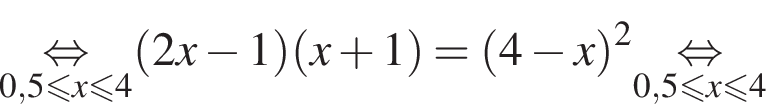
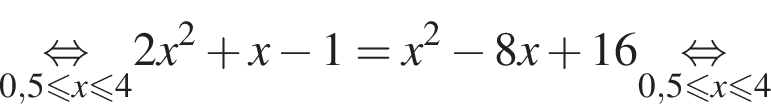
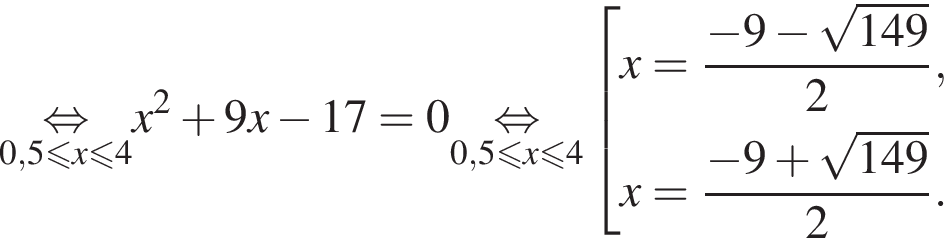
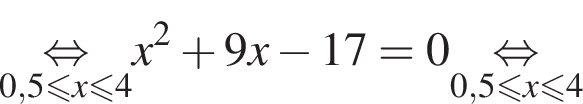
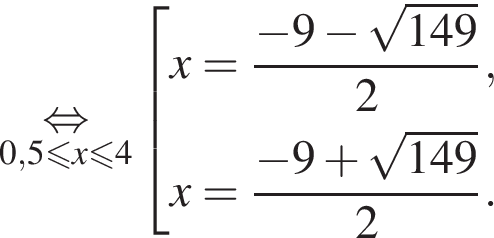
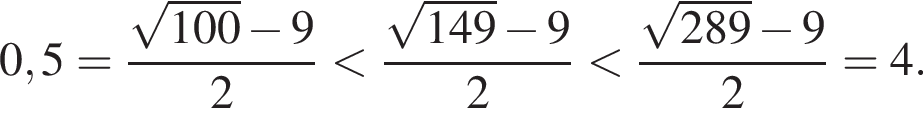
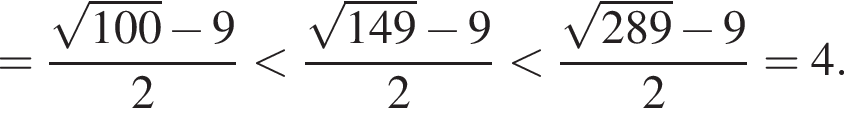
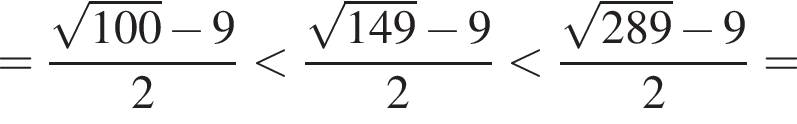
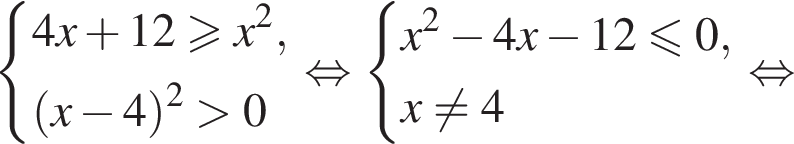
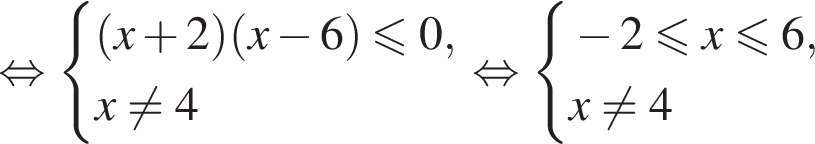
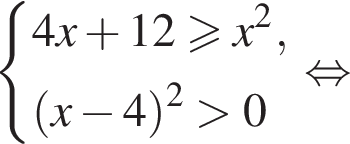
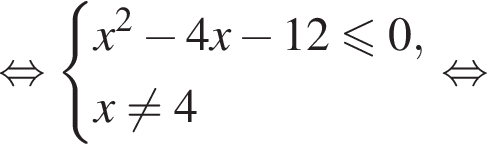
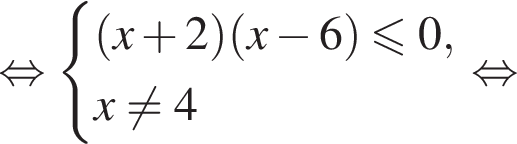
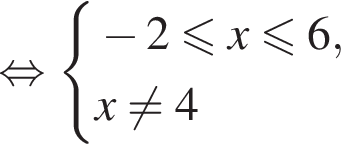
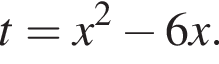 Тогда:
Тогда: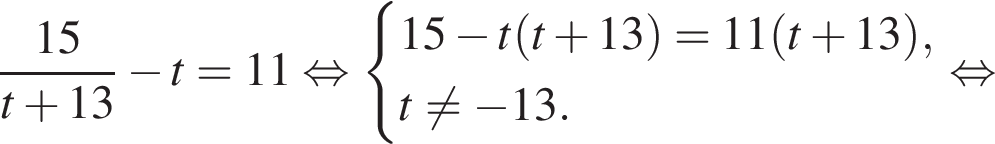
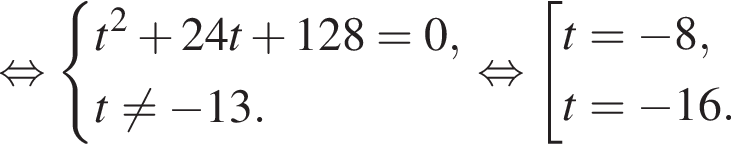
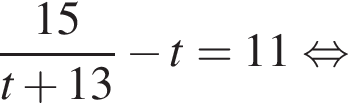
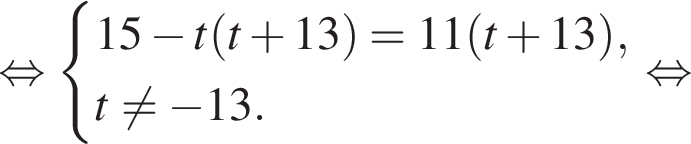
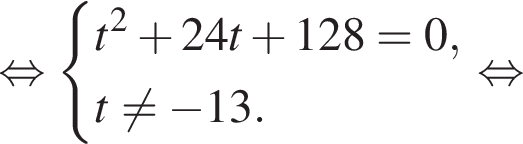
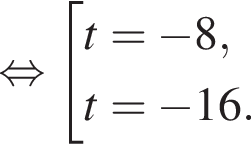
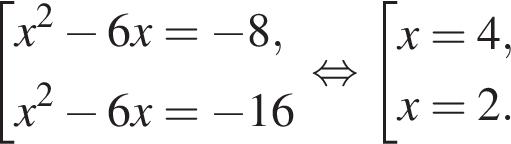
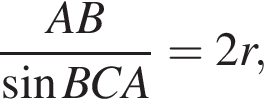 откуда
откуда 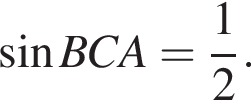 Из прямоугольного треугольника BHC имеем:
Из прямоугольного треугольника BHC имеем: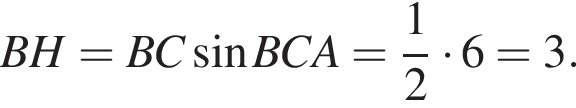
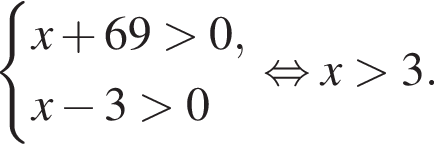
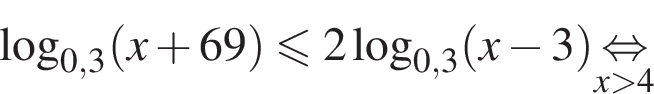
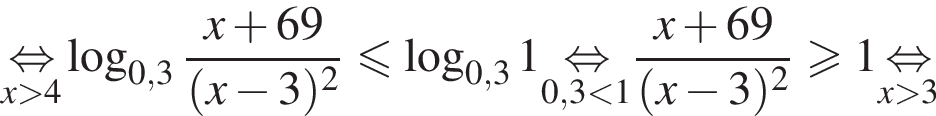
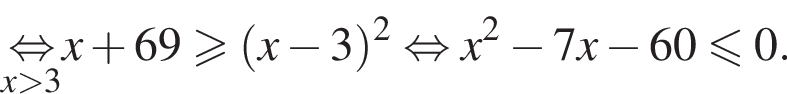
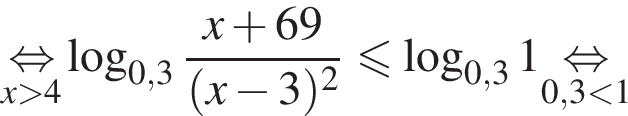
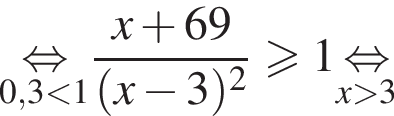
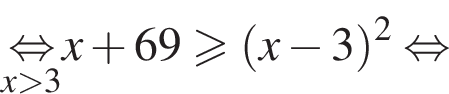
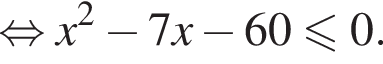
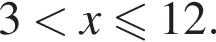 Наименьшее целое решение неравенства — число 4, наибольшее целое решение — число 12, их сумма равна 16.
Наименьшее целое решение неравенства — число 4, наибольшее целое решение — число 12, их сумма равна 16.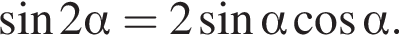 Тогда:
Тогда: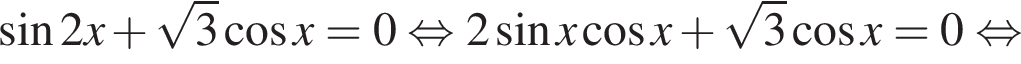
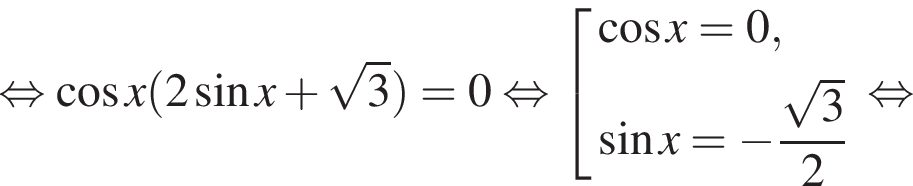
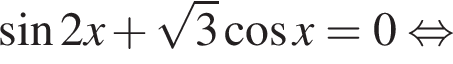
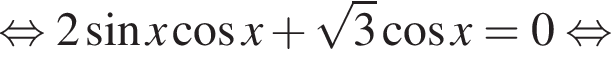
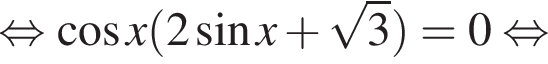
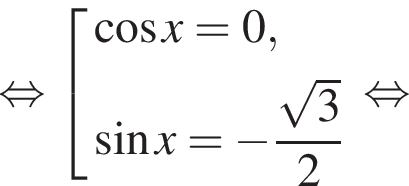
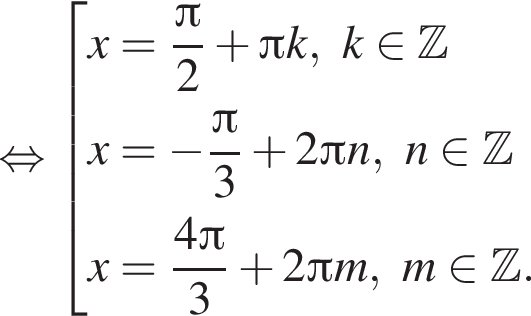
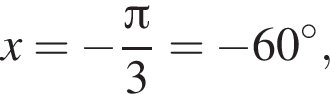 наименьшим положительным решением уравнения является корень
наименьшим положительным решением уравнения является корень 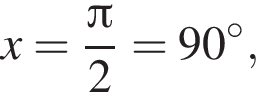 их сумма равна 30°.
их сумма равна 30°.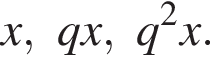
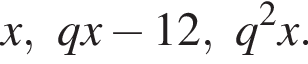
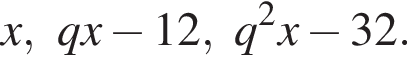
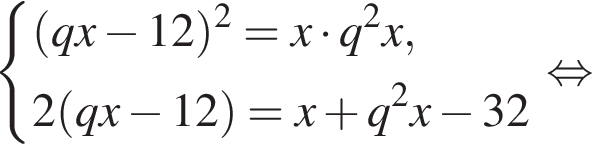
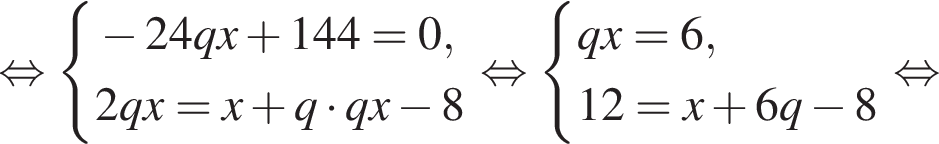
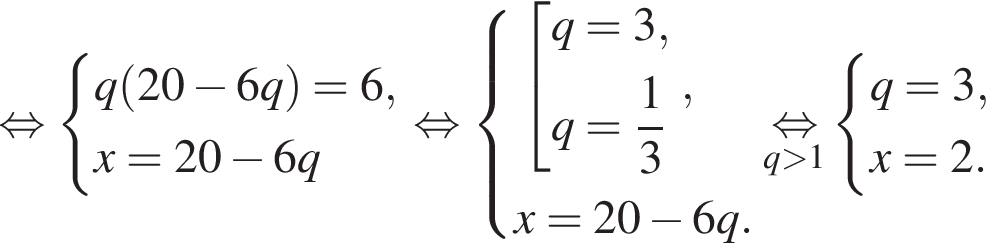
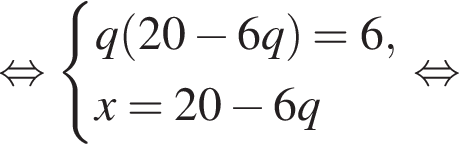
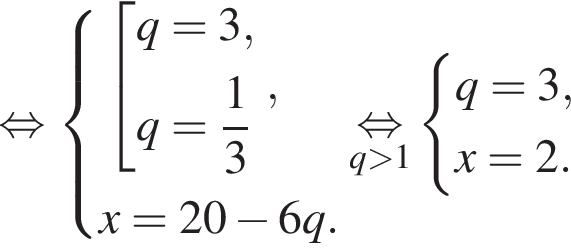
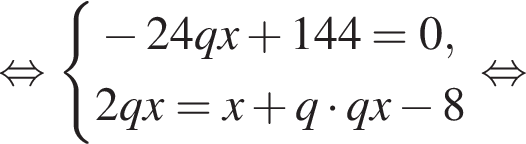
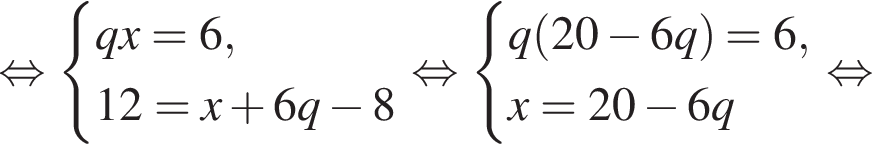
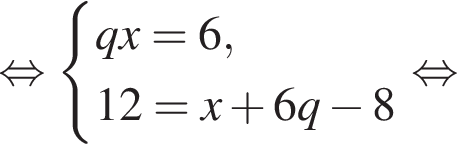
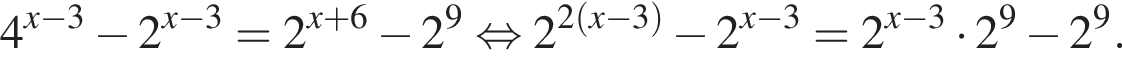
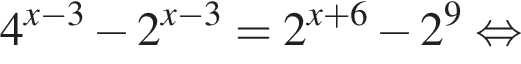
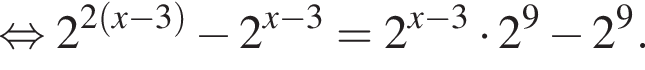
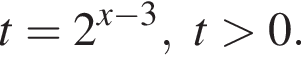 Поэтому:
Поэтому: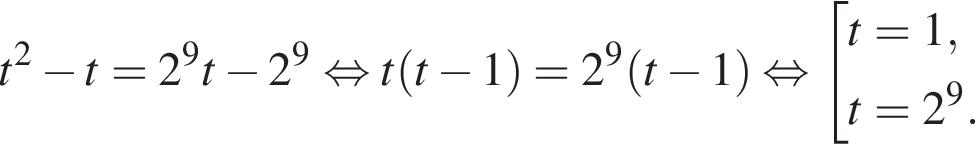
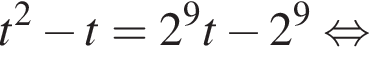
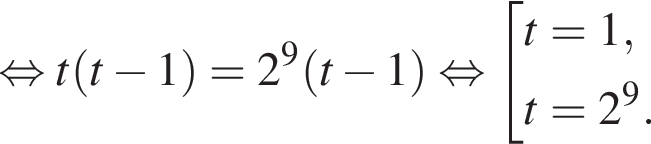
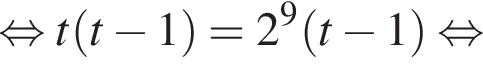
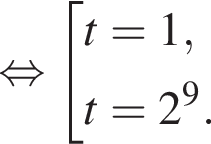
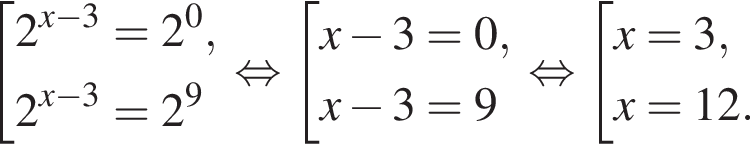
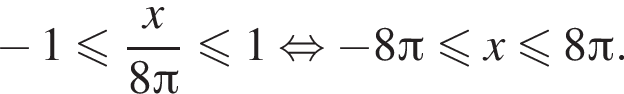
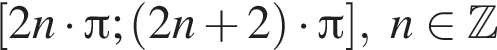 вплоть до
вплоть до 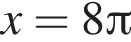 решений нет. Поэтому на положительной полуоси уравнение имеет 8 решений. В силу четности левой и правой частей уравнения всего имеем 16 решения.
решений нет. Поэтому на положительной полуоси уравнение имеет 8 решений. В силу четности левой и правой частей уравнения всего имеем 16 решения. совпадает со знаком разности
совпадает со знаком разности  имеем:
имеем: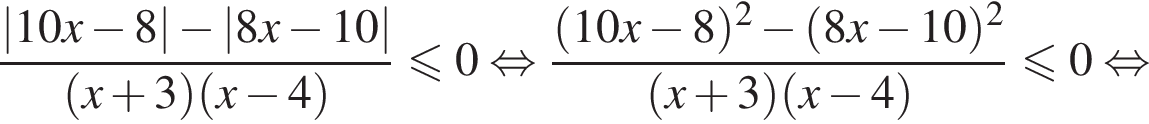
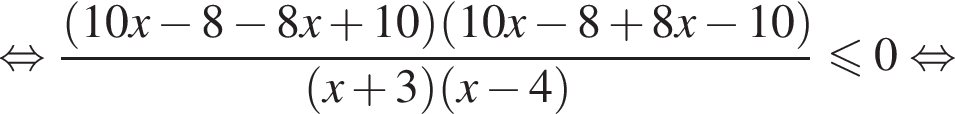
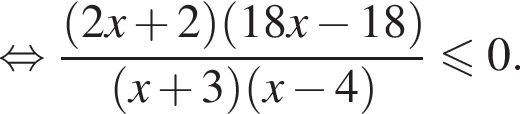
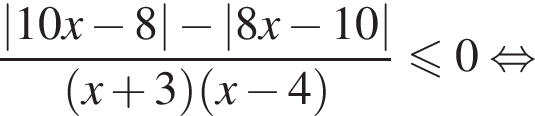
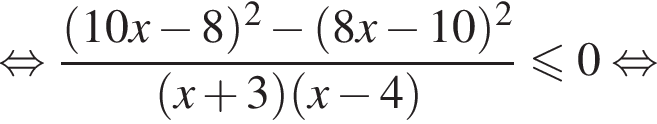
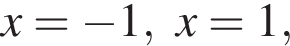 корни знаменателя
корни знаменателя 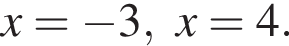 Поэтому:
Поэтому: 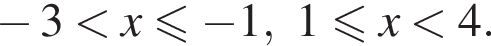 Целые решения — числа −2, -1, 1, 2, 3. Их сумма равна 3.
Целые решения — числа −2, -1, 1, 2, 3. Их сумма равна 3.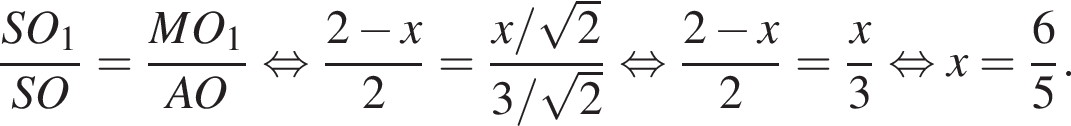
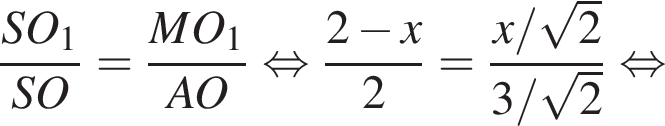
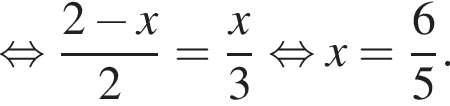
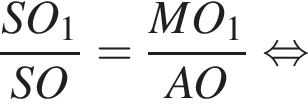
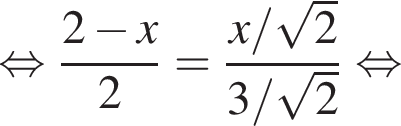
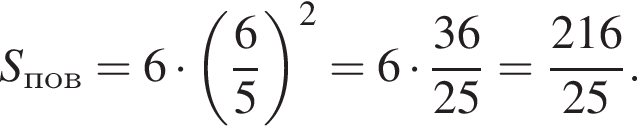
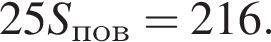
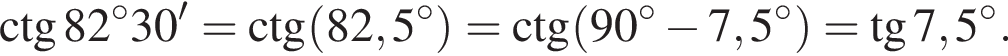
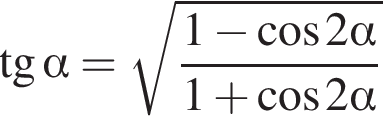 :
: 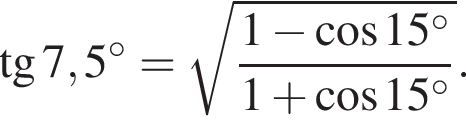



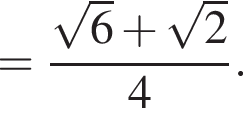
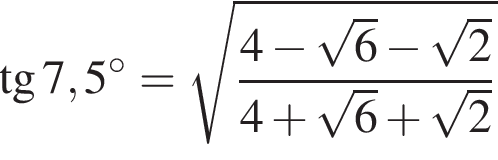
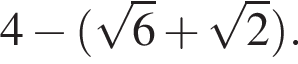 Тогда:
Тогда: 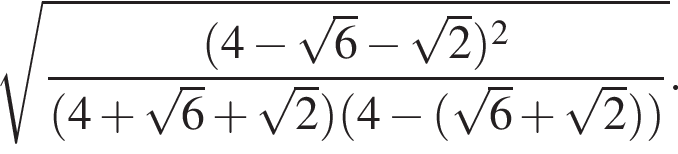
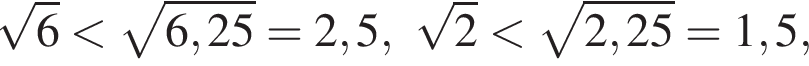
 тогда
тогда 
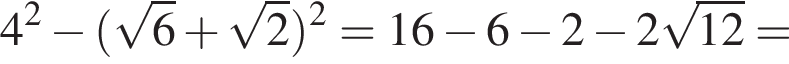

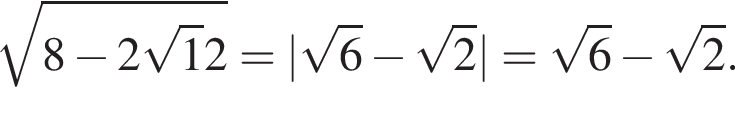 Тогда:
Тогда: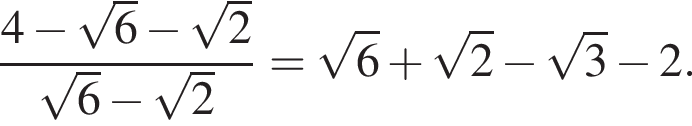
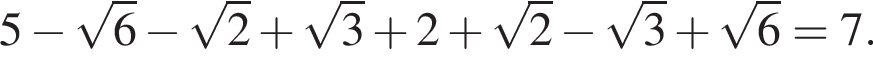
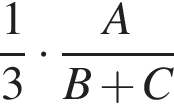 работы.
работы. 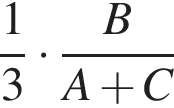 работы.
работы. 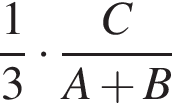 работы.
работы. 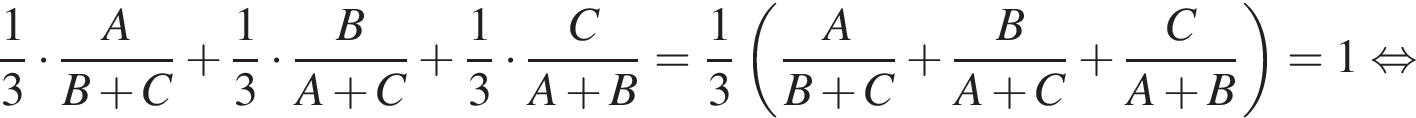
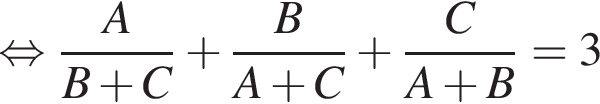
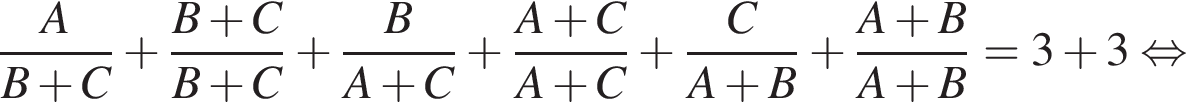
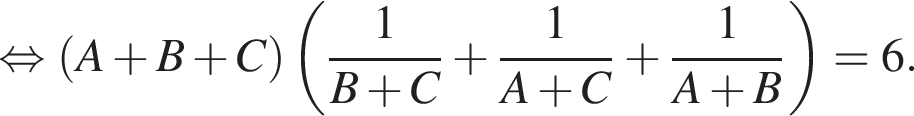
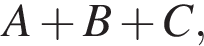 то они выполнили бы работу за:
то они выполнили бы работу за: 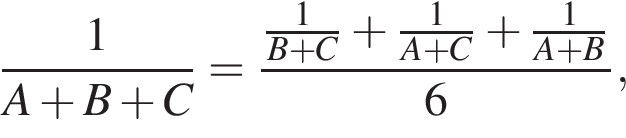
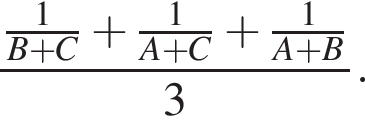 Поэтому, работая вместе работа была бы выполнена в
Поэтому, работая вместе работа была бы выполнена в 